画图并填空：
（1）画出图中△ABC的高AD（标注出点D的位置）；
（2）画出把△ABC沿射线AD方向平移3cm后得到的△A1B1C1；
（3）根据“图形平移”的性质，得BB1= cm，AC与A1C1的位置关系是：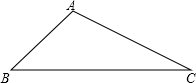 
相关试题
某旅行社为吸引市民组团去千岛湖旅游，推出如下收费标准：
某单位组织员工去千岛湖旅游，共支付给该旅行社旅游费用27000 元，请问该单位这次共有多少员工去旅游？
推荐套卷
画图并填空：
（1）画出图中△ABC的高AD（标注出点D的位置）；
（2）画出把△ABC沿射线AD方向平移3cm后得到的△A1B1C1；
（3）根据“图形平移”的性质，得BB1= cm，AC与A1C1的位置关系是：
某旅行社为吸引市民组团去千岛湖旅游，推出如下收费标准：
某单位组织员工去千岛湖旅游，共支付给该旅行社旅游费用27000 元，请问该单位这次共有多少员工去旅游？
粤公网安备 44130202000953号