甲、乙、丙三人中要选一人去参加唱歌比赛，于是他们制定了一个规则，规则为：(如图)以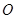
为起点，再从
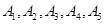，这
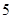个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为
，若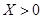
就让甲去；若
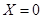就让乙去；若
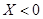就是丙去.
（Ⅰ）写出数量积的所有可能取值；
（Ⅱ）求甲、乙、丙三人去参加比赛的概率，并由求出的概率来说明这个规则公平吗？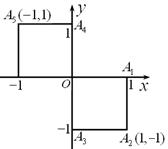
相关试题
的底面为直角梯形，
，
底面
，且
，
，
是
的中点。
面
；
与
与面
所成二面角的余弦值.
，点
.
，项数为偶数，如果其奇数项的和为
，偶数项的和为
，求此数列的公比和项数.推荐套卷
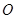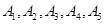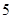甲、乙、丙三人中要选一人去参加唱歌比赛，于是他们制定了一个规则，规则为：(如图)以为起点，再从，这个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为，若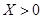就让甲去；若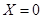就让乙去；若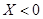就是丙去.
（Ⅰ）写出数量积的所有可能取值；
（Ⅱ）求甲、乙、丙三人去参加比赛的概率，并由求出的概率来说明这个规则公平吗？
粤公网安备 44130202000953号