为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?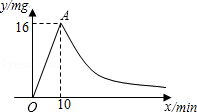
相关知识点
推荐套卷
为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比,燃烧后,y与x成反比(如图),现测得药物10min燃烧完,此时,教室内每立方米空气含药量为16mg.已知每立方米空气中含药量低于4mg时对人体无害,那么从消毒开始经多长时间后学生才能进教室?