为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 
请根据以上图表提供的信息,解答下列问题:
(1)在女生身高频数分布表中: = ,
= , = ,
= , = ;
= ;
(2)补全男生身高频数分布直方图;
(3)已知该校共有女生400人,男生380人,请估计身高在165≤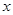 <170之间的学生约有多少人.
<170之间的学生约有多少人.
相关知识点
推荐套卷
为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 
请根据以上图表提供的信息,解答下列问题:
(1)在女生身高频数分布表中: = ,
= , = ,
= , = ;
= ;
(2)补全男生身高频数分布直方图;
(3)已知该校共有女生400人,男生380人,请估计身高在165≤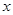 <170之间的学生约有多少人.
<170之间的学生约有多少人.