某公司要把240吨白砂糖运往某市的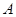
、
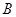两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往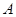地的运费为：大车630元/辆，小车420元/辆；运往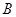地的运费为：大车750元/辆，小车550元/辆.
（1）求两种货车各用多少辆；
（2）如果安排10辆货车前往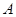地，其中调往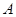地的大车有
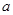辆，其余货车前往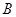地，若设总运费为
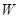，求W与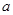的关系式（用含有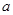的代数式表示W）.
相关知识点
推荐套卷
某公司要把240吨白砂糖运往某市的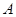、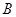两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖.已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往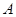地的运费为：大车630元/辆，小车420元/辆；运往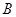地的运费为：大车750元/辆，小车550元/辆.
（1）求两种货车各用多少辆；
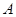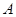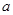（2）如果安排10辆货车前往地，其中调往地的大车有辆，其余货车前往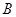地，若设总运费为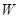，求W与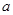的关系式（用含有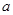的代数式表示W）.
粤公网安备 44130202000953号