在平面直角坐标系
中，点M（
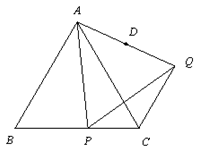
,），以点M为圆心，OM长为半径作⊙M ，使⊙M与直线OM的另一交点为点B，与
轴，
轴的另一交点分别为点D，A（如图），连接AM.点P是
上的动点.
（1）写出∠AMB的度数；
（2）点Q在射线OP上，且OP·OQ=20，过点Q作QC垂直于直线OM，垂足为C，直线QC交轴于点E.
①当动点P与点B重合时，求点E的坐标；
②连接QD，设点Q的纵坐标为t，△QOD的面积为S，求S与t的函数关系式及S的取值范围.
相关试题
是
外任意一点，过点
，
，分别交
，
，
，
．求证：
（
的度数
的度数）．
为
的直径，
，垂足为
，
，
与
交于
．
；
，
把半圆三等分，
，求
的长．
为锐角三角形，△
，
，
是△
是
的直径．求证：
．
中，弦
为直径，
于点
，
，
，求
和
.
相关知识点
推荐套卷
粤公网安备 44130202000953号