如图1,在矩形ABCD中,AB=4,AD=2,点P是边AB上的一个动点(不与点A、点B重合),点Q在边AD上,将△CBP和△QAP分别沿PC、PQ折叠,使B点与E点重合,A点与F点重合,且P、E、F三点共线.
(1)若点E平分线段PF,则此时AQ的长为多少?
(2)若线段CE与线段QF所在的平行直线之间的距离为2,则此时AP的长为多少?
(3)在“线段CE”、“线段QF”、“点A”这三者中,是否存在两个在同一条直线上的情况?若存在,求出此时AP的长;若不存在,请说明理由.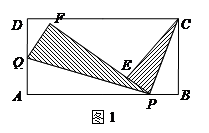

相关知识点
推荐套卷
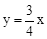 以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).
以每秒0.6个单位的速度向上平移,分别交AO、BO于点C、D,设运动时间为t秒(0<t<5).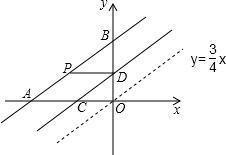
 销售量】
销售量】 粤公网安备 44130202000953号
粤公网安备 44130202000953号