为了响应岳阳市政府“低碳出行、绿色出行”的号召，某中学数学兴趣小组在全校2000名学生中就上学方式随机抽取了400名学生进行抽样调查，经统计整理绘制出图a、图b两幅不完整的统计图：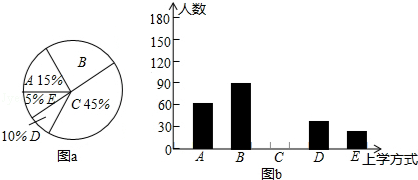
A：步行；B：骑自行车；C：乘公共交通工具；D：乘私家车；E：其他．
请根据统计图提供的信息解答下列问题：
（1）图a中“B”所在扇形的圆心角为 ；
（2）请在图b中把条形统计图补充完整；
（3）请根据样本数据估计全校骑自行车上学的学生人数．
相关试题
为了解某品牌电风扇销售量的情况，对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售
量进行统计，绘制如下两个统计图（均不完整）．请你结合图中的信息,解答下列问题:
（1）该商场5月份售出这种品牌的电风扇共多少台?
（2）若该商场计划订购这三种型号的电风扇共2000台，根据5月份销售量的情况，求该商场应订购丙种型号电风扇多少台比较合理？ 
从甲学校到乙学校有
、
、
三条线路，从乙学校到丙学校有
、
二条线路．
（1）利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果；
（2）小张任意走了一条从甲学校到丙学校的线路，求小张恰好经过了线路的概率是多少？
.请你画出旋转后的△
． 
相关知识点
推荐套卷
粤公网安备 44130202000953号