抛物线y2＝2px（p＞0）上纵坐标为－p的点M到焦点的距离为2．
（1）求p的值；
（2）如图，A，B，C为抛物线上三点，且线段MA，MB，MC 与x轴交点的横坐标依次组成公差为1的等差数列，若△AMB的面积是△BMC面积的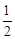
，求直线MB的方程．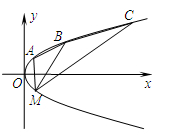
相关试题
的极小值为
，其导函数
的图像开口向下且经过点
，
.
的解析式；
都有
恒成立，求实数
的取值范围．
中，
， 
，
为
中点，
为
中点，且△
为正三角形。
∥平面
； 
⊥平面
中，已知点
在函数
的图像上，且
．
，求数列
的前
项和
．
的方程为：
直线
过点
（1，2），且与圆
、
两点，若
求直线
．
的最小正周期和单调递增区间；
时，求相关知识点
推荐套卷
抛物线y2＝2px（p＞0）上纵坐标为－p的点M到焦点的距离为2．
（1）求p的值；
（2）如图，A，B，C为抛物线上三点，且线段MA，MB，MC 与x轴交点的横坐标依次组成公差为1的等差数列，若△AMB的面积是△BMC面积的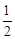，求直线MB的方程．
粤公网安备 44130202000953号