“肇实,正名芡实,因肇庆所产之芡实颗粒大、药力强,故名。”某科研所为进一步改良肇实,为此对肇实的两个品种(分别称为品种A和品种B)进行试验.选取两大片水塘,每大片水塘分成n小片水塘,在总共2n小片水塘中,随机选n小片水塘种植品种A,另外n小片水塘种植B.
(1)假设n=4,在第一大片水塘中,种植品种A的小片水塘的数目记为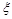 ,求
,求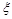 的分布列和数学期望;
的分布列和数学期望;
(2)试验时每大片水塘分成8小片,即n=8,试验结束后得到品种A和品种B在每个小片水塘上的每亩产量(单位:kg/亩)如下表:
号码
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
品种A
|
101
|
97
|
92
|
103
|
91
|
100
|
110
|
106
|
品种B
|
115
|
107
|
112
|
108
|
111
|
120
|
110
|
113
|
分别求品种A和品种B的每亩产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?