椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点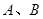
是它的焦点,长轴长为
,焦距为
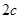,静放在点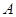
的小球(小球的半径忽略不计)从点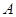沿直线出发,经椭圆壁反射后第一次回到点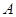时,小球经过的路程是 .
,π<2θ<2π,化简
= .
的单调递增区间为 .
,cosβ=
),则α+β= .推荐套卷
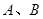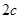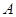椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点是它的焦点,长轴长为,焦距为,静放在点的小球(小球的半径忽略不计)从点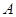沿直线出发,经椭圆壁反射后第一次回到点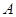时,小球经过的路程是 .
粤公网安备 44130202000953号