如图，某单位准备修建一个面积为600平方米的矩形场地（图中
）的围墙，且要求中间用围墙
隔开，使得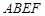
为矩形，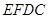
为正方形，设
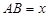米，已知围墙（包括）的修建费用均为800元每米，设围墙（包括）的修建总费用为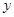
元。
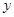（1）求出关于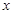
的函数解析式；
（2）当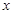为何值时，设围墙（包括）的的修建总费用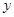最小？并求出的最小值。
相关试题
，函数
.
的值；
的单调区间.
的前
项和为
，公差
，
，且
成等比数列.
的前
中，角A、B，C，所对的边分别为
，且
的值；
，求
，
的值；
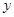的最大值和最小值.
的最小值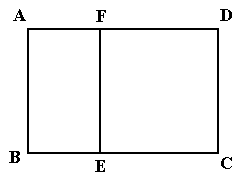．推荐套卷
如图，某单位准备修建一个面积为600平方米的矩形场地（图中）的围墙，且要求中间用围墙隔开，使得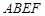为矩形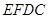，为正方形，设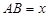米，已知围墙（包括）的修建费用均为800元每米，设围墙（包括）的修建总费用为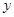元。
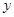（1）求出关于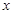的函数解析式；
（2）当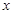为何值时，设围墙（包括）的的修建总费用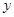最小？并求出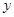的最小值。
粤公网安备 44130202000953号