已知函数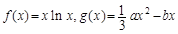
，其中a，b∈R
(1)求函数f(x)的最小值；
(2)当a＞0，且a为常数时，若函数h(x)＝x[g(x)＋1]对任意的x1＞x2≥4，总有
成立，试用a表示出b的取值范围；
(3)当
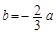时，若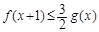
对x∈[0，＋∞)恒成立，求a的最小值.
相关试题
，且满足
，
.
，求
的值.
+b+c
在
处取得极值,并且它的图象与直线
在点( 1 , 0
) 处相
切, 求a , b , c的值。
是直径)；
.推荐套卷
已知函数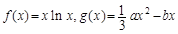，其中a，b∈R
(1)求函数f(x)的最小值；
(2)当a＞0，且a为常数时，若函数h(x)＝x[g(x)＋1]对任意的x1＞x2≥4，总有成立，试用a表示出b的取值范围；
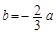(3)当时，若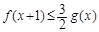对x∈[0，＋∞)恒成立，求a的最小值.
粤公网安备 44130202000953号