已知点A(-1,0),B(1,-1)和抛物线.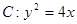 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(1)证明:  为定值;
为定值;
(2)若△POM的面积为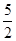 ,求向量
,求向量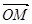 与
与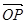 的夹角;
的夹角;
(3)证明直线PQ恒过一个定点.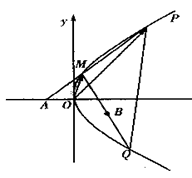
相关知识点
推荐套卷
已知点A(-1,0),B(1,-1)和抛物线.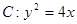 ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(1)证明:  为定值;
为定值;
(2)若△POM的面积为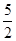 ,求向量
,求向量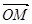 与
与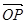 的夹角;
的夹角;
(3)证明直线PQ恒过一个定点.