对于三次函数
 。
。
定义:(1)设 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解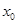 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设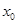 为常数,若定义在
为常数,若定义在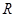 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数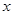 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数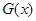 ,使得它的“拐点”是
,使得它的“拐点”是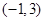 (不要过程)
(不要过程)
推荐套卷
对于三次函数
 。
。
定义:(1)设 是函数
是函数 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解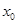 ,则称点
,则称点 为函数
为函数 的“拐点”;
的“拐点”;
定义:(2)设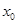 为常数,若定义在
为常数,若定义在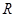 上的函数
上的函数 对于定义域内的一切实数
对于定义域内的一切实数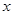 ,都有
,都有 成立,则函数
成立,则函数 的图象关于点
的图象关于点 对称。
对称。
己知 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2)检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数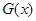 ,使得它的“拐点”是
,使得它的“拐点”是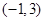 (不要过程)
(不要过程)