已知直线y=﹣x+1与椭圆
+
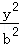=1（a＞b＞0）相交于A、B两点．
①若椭圆的离心率为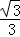
，焦距为2，求线段AB的长；
②若向量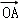
与向量
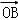互相垂直（其中O为坐标原点），当椭圆的离心率e∈[
，
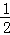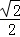]时，求椭圆的长轴长的最大值．
推荐套卷
已知直线y=﹣x+1与椭圆+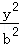=1（a＞b＞0）相交于A、B两点．
①若椭圆的离心率为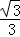，焦距为2，求线段AB的长；
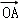②若向量与向量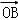互相垂直（其中O为坐标原点），当椭圆的离心率e∈[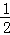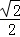，]时，求椭圆的长轴长的最大值．
粤公网安备 44130202000953号