某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛，其得分情况如茎叶图所示：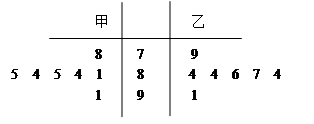
（1）若从甲运动员的不低于80且不高于90的得分中任选3个，求其中与平均得分之差的绝对值不超过2的概率；
（2）若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个，求甲、乙两名运动员得分之差的绝对值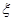
的分布列与期望.
相关试题
的图象在点
处的切线方程为
。
的解析式；
在区间
上恰有两个相异实根，求m的取值范围。
中，角A,B,C所对的边分别是
，且
。
，求周长
的最大值。
，且
。
时，且
，求x的值；
，求
的单调递增区间。
，且
。求
的值。
定义在区间
上，
，且当
时，恒有
．又数列
满足
．
的表达式；
为数列
的前
项和，若
对
恒成立，求
的最小值．推荐套卷
某地为迎接2014年索契冬奥会,举行了一场奥运选拔赛,其中甲、乙两名运动员为争取最后一个参赛名额进行的7轮比赛，其得分情况如茎叶图所示：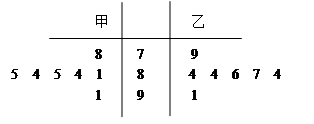
（1）若从甲运动员的不低于80且不高于90的得分中任选3个，求其中与平均得分之差的绝对值不超过2的概率；
（2）若分别从甲、乙两名运动员的每轮比赛不低于80且不高于90的得分中任选1个，求甲、乙两名运动员得分之差的绝对值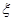的分布列与期望.
粤公网安备 44130202000953号