已知抛物线 的焦点
的焦点 到准线的距离为
到准线的距离为 .过点
.过点

作直线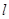 交抛物线
交抛物线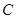 与
与 两点(
两点( 在第一象限内).
在第一象限内).
(1)若 与焦点
与焦点 重合,且
重合,且 .求直线
.求直线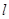 的方程;
的方程;
(2)设 关于
关于 轴的对称点为
轴的对称点为 .直线
.直线 交
交 轴于
轴于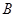 . 且
. 且 .求点
.求点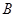 到直线
到直线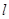 的距离的取值范围.
的距离的取值范围.
相关知识点
推荐套卷
已知抛物线 的焦点
的焦点 到准线的距离为
到准线的距离为 .过点
.过点

作直线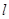 交抛物线
交抛物线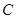 与
与 两点(
两点( 在第一象限内).
在第一象限内).
(1)若 与焦点
与焦点 重合,且
重合,且 .求直线
.求直线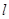 的方程;
的方程;
(2)设 关于
关于 轴的对称点为
轴的对称点为 .直线
.直线 交
交 轴于
轴于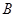 . 且
. 且 .求点
.求点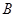 到直线
到直线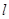 的距离的取值范围.
的距离的取值范围.