设非常数数列{an}满足
，n∈N*，其中常数α，β均为非零实数，且 α＋β≠0.
（1）证明：数列{an}为等差数列的充要条件是α＋2β＝0；
（2）已知α＝1，β＝
， a1＝1，a2＝
，求证：数列{| an＋1－an－1|} (n∈N*，n≥2)与数列{n＋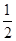
} (n∈N*)中没有相同数值的项.
相关试题
,若
=
时，求
上的取值范围；
时，
，求
的值．
：不等式
恒成立 ；命题
：函数
的定义域为
，若“
”为真，“
”为假，求
的取值范围。
，B＝
．
B；
的实数a的取值范围．
的最大值.
的各条棱长都为a，P为
上的点。
的值，使得PC⊥AB；
，求二面角P—AC—B的大小；
到平面PAC的距离。
推荐套卷
设非常数数列{an}满足，n∈N*，其中常数α，β均为非零实数，且 α＋β≠0.
（1）证明：数列{an}为等差数列的充要条件是α＋2β＝0；
（2）已知α＝1，β＝， a1＝1，a2＝，求证：数列{| an＋1－an－1|} (n∈N*，n≥2)与数列{n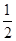＋} (n∈N*)中没有相同数值的项.
粤公网安备 44130202000953号