在平面直角坐标系xOy中，如图，已知椭圆C：
＋
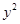＝1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y＝－2分别交于点M、N.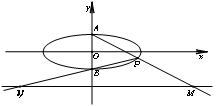
（1）设直线AP、PB的斜率分别为k1，k2，求证：k1·k2为定值；
（2）求线段MN长的最小值；
（3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．
相关试题
,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。
C． C
D推荐套卷
在平面直角坐标系xOy中，如图，已知椭圆C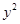：＋＝1的上、下顶点分别为A、B，点P在椭圆C上且异于点A、B，直线AP、PB与直线l：y＝－2分别交于点M、N.
（1）设直线AP、PB的斜率分别为k1，k2，求证：k1·k2为定值；
（2）求线段MN长的最小值；
（3）当点P运动时，以MN为直径的圆是否经过某定点？请证明你的结论．
粤公网安备 44130202000953号