设椭圆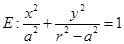 的焦点在
的焦点在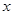 轴上,
轴上, 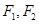 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点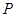 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线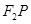 交
交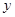 轴于点
轴于点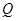 ,
,
(1)当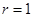 时,
时,
(1)若椭圆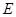 的离心率为
的离心率为 ,求椭圆
,求椭圆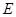 的方程;
的方程;
(2)当点P在直线 上时,求直线
上时,求直线 与
与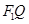 的夹角;
的夹角;
(2) 当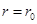 时,若总有
时,若总有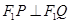 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).
推荐套卷
设椭圆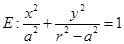 的焦点在
的焦点在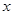 轴上,
轴上, 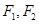 分别是椭圆的左、右焦点,点
分别是椭圆的左、右焦点,点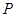 是椭圆在第一象限内的点,直线
是椭圆在第一象限内的点,直线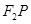 交
交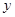 轴于点
轴于点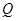 ,
,
(1)当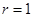 时,
时,
(1)若椭圆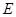 的离心率为
的离心率为 ,求椭圆
,求椭圆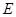 的方程;
的方程;
(2)当点P在直线 上时,求直线
上时,求直线 与
与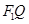 的夹角;
的夹角;
(2) 当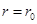 时,若总有
时,若总有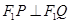 ,猜想:当
,猜想:当 变化时,点
变化时,点 是否在某定直线上,若是写出该直线方程(不必求解过程).
是否在某定直线上,若是写出该直线方程(不必求解过程).