已知椭圆 :
: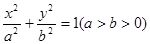 的短轴长为
的短轴长为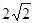 ,且斜率为
,且斜率为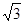 的直线
的直线 过椭圆
过椭圆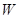 的焦点及点
的焦点及点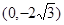 .
.
(1)求椭圆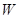 的方程;
的方程;
(2)已知直线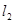 过椭圆
过椭圆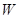 的左焦点
的左焦点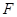 ,交椭圆于点P、Q.
,交椭圆于点P、Q.
(ⅰ)若满足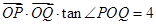 (
(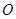 为坐标原点),求
为坐标原点),求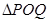 的面积;
的面积;
(ⅱ)若直线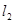 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点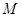 在
在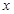 轴上,且使
轴上,且使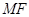 为
为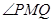 的一条角平分线,则称点
的一条角平分线,则称点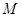 为椭圆
为椭圆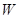 的“特征点”,求椭圆
的“特征点”,求椭圆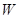 的特征点.
的特征点.
推荐套卷
已知椭圆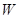 :
: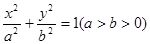 的短轴长为
的短轴长为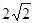 ,且斜率为
,且斜率为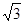 的直线
的直线 过椭圆
过椭圆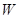 的焦点及点
的焦点及点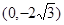 .
.
(1)求椭圆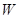 的方程;
的方程;
(2)已知直线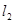 过椭圆
过椭圆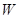 的左焦点
的左焦点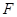 ,交椭圆于点P、Q.
,交椭圆于点P、Q.
(ⅰ)若满足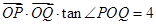 (
(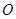 为坐标原点),求
为坐标原点),求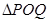 的面积;
的面积;
(ⅱ)若直线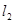 与两坐标轴都不垂直,点
与两坐标轴都不垂直,点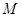 在
在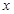 轴上,且使
轴上,且使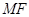 为
为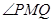 的一条角平分线,则称点
的一条角平分线,则称点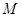 为椭圆
为椭圆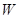 的“特征点”,求椭圆
的“特征点”,求椭圆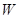 的特征点.
的特征点.