设M、N为抛物线C：y＝x2上的两个动点，过M、N分别作抛物线C的切线l1、l2，与x轴分别交于A、B两点，且l1与l2相交于点P，若|AB|＝1．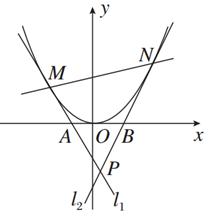
(1)求点P的轨迹方程；
(2)求证：△MNP的面积为一个定值，并求出这个定值．
相关试题
的方程
的两根为
和
：(12分)
的值；
的值．
,求
的值.
相关知识点
推荐套卷
设M、N为抛物线C：y＝x2上的两个动点，过M、N分别作抛物线C的切线l1、l2，与x轴分别交于A、B两点，且l1与l2相交于点P，若|AB|＝1．
(1)求点P的轨迹方程；
(2)求证：△MNP的面积为一个定值，并求出这个定值．
粤公网安备 44130202000953号