如图,四棱柱中,底面.四边形为梯形,,且.过三点的平面记为 ,
,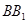 与的交点为.
与的交点为.
(1)证明:为的中点;
(2)求此四棱柱被平面所分成上下两部分的体积之比;
(3)若,梯形的面积为6,求平面与底面所成二面角大小.

相关知识点
推荐套卷
如图,四棱柱中,底面.四边形为梯形,,且.过三点的平面记为 ,
,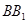 与的交点为.
与的交点为.
(1)证明:为的中点;
(2)求此四棱柱被平面所分成上下两部分的体积之比;
(3)若,梯形的面积为6,求平面与底面所成二面角大小.
