某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为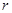 米,高为
米,高为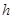 米,体积为
米,体积为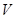 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为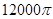 元(
元(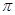 为圆周率).
为圆周率).
(1)将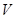 表示成
表示成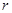 的函数
的函数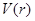 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数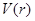 的单调性,并确定
的单调性,并确定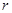 和
和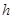 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.
推荐套卷
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为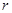 米,高为
米,高为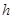 米,体积为
米,体积为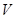 立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为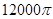 元(
元(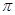 为圆周率).
为圆周率).
(1)将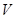 表示成
表示成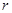 的函数
的函数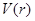 ,并求该函数的定义域;
,并求该函数的定义域;
(2)讨论函数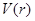 的单调性,并确定
的单调性,并确定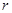 和
和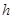 为何值时该蓄水池的体积最大.
为何值时该蓄水池的体积最大.