已知定点F(0，1)和直线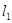
：y＝－1，过定点F与直线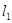相切的动圆圆心为点C.
(1)求动点C的轨迹方程；
(2)过点F的直线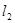
交动点C的轨迹于两点P、Q，交直线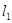于点R，求
·
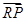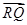的最小值；
(3)过点F且与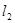垂直的直线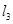
交动点C的轨迹于两点R、T，问四边形PRQT的面积是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．
,且
，求证：
.
在
处取得极值－2.
的解析式； 
在点
处的切线方程.
求证：
.
的单调区间;
上的最小值;
,
恒成立,求实数
的取值范围．相关知识点
推荐套卷
已知定点F(0，1)和直线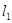：y＝－1，过定点F与直线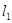相切的动圆圆心为点C.
(1)求动点C的轨迹方程；
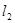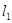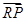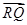(2)过点F的直线交动点C的轨迹于两点P、Q，交直线于点R，求·的最小值；
(3)过点F且与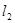垂直的直线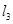交动点C的轨迹于两点R、T，问四边形PRQT的面积是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．
粤公网安备 44130202000953号