(本小题满分12分)一工厂生产甲、乙、丙三种样式的杯子,每种样式均有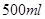 和
和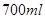 两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取
两种型号,某天的产量如右表(单位:个):按样式分层抽样的方法在这个月生产的杯子中抽取 个,其中有甲样式杯子
个,其中有甲样式杯子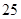 个.
个.
| 型号 |
甲样式 |
乙样式 |
丙样式 |
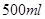 |
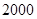 |
 |
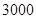 |
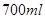 |
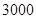 |
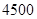 |
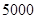 |
(1)求 的值;
的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为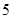 的样本,从这个样本中任取
的样本,从这个样本中任取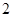 个杯子,求至少有
个杯子,求至少有 个
个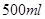 杯子的概率.
杯子的概率.
相关知识点
推荐套卷
 命题q:1-m≤x≤1+m,m>0,
命题q:1-m≤x≤1+m,m>0,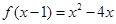 ,求函数
,求函数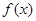 ,
,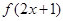 的解析式.
的解析式.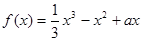 (
(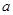 为常数)
为常数)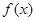 在区间
在区间 上单调递减,求
上单调递减,求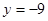 相切:
相切: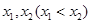 处取得极值,记点M (
处取得极值,记点M ( ,
,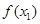 ),N(
),N(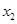 ,
,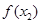 ),P(
),P(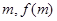 ),
),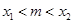 , 若对任意的m
, 若对任意的m 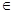 (
( , x
, x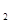 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定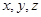 满足
满足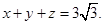
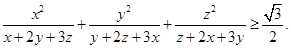
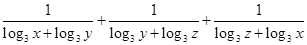 的最小值.
的最小值.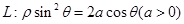 外的一点
外的一点 (其中
(其中 为锐角)作平行于
为锐角)作平行于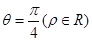 的直线
的直线 与曲线分别交于
与曲线分别交于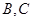 .
. 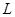 和直线
和直线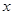 轴的正半轴建系);
轴的正半轴建系); 成等比数列,求
成等比数列,求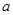 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号