现在“校园手机”越来越受到社会的关注,我校学生处随机调查了本校若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下统计图: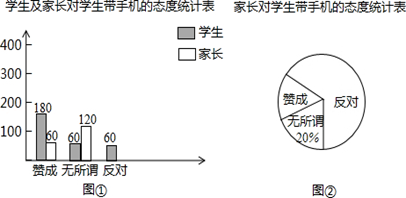
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的家长来看,若该校的家长为2500名,则有多少名家长持反对态度?
相关知识点
推荐套卷
现在“校园手机”越来越受到社会的关注,我校学生处随机调查了本校若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下统计图:
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)从这次接受调查的家长来看,若该校的家长为2500名,则有多少名家长持反对态度?