如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，
分别为
的中点，
分别为
，
的中点．
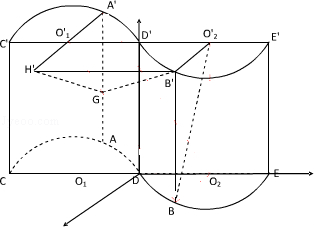
（1）证明：
四点共面；
（2）设
为
中点，延长
到
，使得
．证明：
平面
.
相关试题
，一个焦点是F（0，1）．
过点F交椭圆于A、B两点，且
，求直线
时,求函数
的最小值;
,
恒成立,试求实数
的取值范围.
，
的等比中项。
是等差数列；
的前n项和为Tn,求Tn。
图象的对称中心的横坐标；
，求函数
的定义域为集合A,函数
的定义域为集合B.
A，求实数
的取值范围。推荐套卷
如图所示的几何体是将高为2，底面半径为1的直圆柱沿过轴的平面切开后，将其中一半沿切面向右水平平移后得到的，
分别为
的中点，
分别为
，
的中点．
（1）证明：
四点共面；
（2）设
为
中点，延长
到
，使得
．证明：
平面
.
粤公网安备 44130202000953号