平面直角坐标系中，如果
与
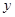都是整数，就称点
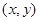为整点，命题：
①存在这样的直线，既不与坐标轴平行又不经过任何整点；
②如果
与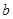
都是无理数，则直线
不经过任何整点；
③如果与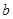都是有理数，则直线必经过无穷多个整点；
④如果直线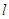
经过两个不同的整点，则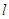必经过无穷多个整点；
⑤存在恰经过一个整点的直线；
其中的真命题是 （写出所有真命题编号）．
的顶点都在半径为4的球
的球面上，且
，
，则棱锥
的体积为 ．
中，
， 
，则
．
、
、
是三角形三个角的弧度数，则
的最小值 ．
的斜率
，经过点
,点
在直线
的数量
为参数，则直线
，它们所对应的点分别为
．若
,则
的值是 ．推荐套卷
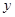平面直角坐标系中，如果与都是整数，就称点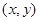为整点，命题：
①存在这样的直线，既不与坐标轴平行又不经过任何整点；
②如果与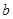都是无理数，则直线不经过任何整点；
③如果与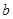都是有理数，则直线必经过无穷多个整点；
④如果直线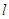经过两个不同的整点，则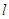必经过无穷多个整点；
⑤存在恰经过一个整点的直线；
其中的真命题是 （写出所有真命题编号）．
粤公网安备 44130202000953号