如图,已知平面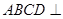 平面
平面 ,且四边形
,且四边形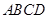 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, ,
,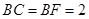 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设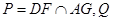 是直线
是直线 上的动点,判断并证明直线
上的动点,判断并证明直线 与直线
与直线 的位置关系.
的位置关系.
(3) 求三棱锥 的体积.[来.
的体积.[来.
相关知识点
推荐套卷
如图,已知平面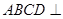 平面
平面 ,且四边形
,且四边形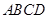 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, ,
,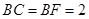 .
.
(1)作出这个几何体的三视图(不要求写作法).
(2)设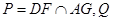 是直线
是直线 上的动点,判断并证明直线
上的动点,判断并证明直线 与直线
与直线 的位置关系.
的位置关系.
(3) 求三棱锥 的体积.[来.
的体积.[来.