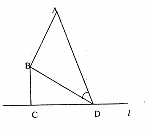
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4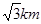 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x>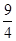 ),点D对跑道AB的视角为
),点D对跑道AB的视角为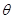 .
.
(1)将tan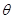 表示为x的函数:
表示为x的函数:
(2)求点D的位置,使得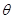 取得最大值.
取得最大值.
推荐套卷
如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在直线与海岸线,的夹角为60°(海岸线看作直线),跑道上距离海岸线最近的点B到海岸线的距离BC=4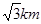 ,D为海岸线l上的一点.设CD=xkm(x>
,D为海岸线l上的一点.设CD=xkm(x>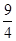 ),点D对跑道AB的视角为
),点D对跑道AB的视角为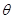 .
.
(1)将tan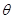 表示为x的函数:
表示为x的函数:
(2)求点D的位置,使得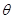 取得最大值.
取得最大值.