数列
的前n项和记为
点
在直线
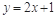上，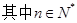
．（1）若数列
是等比数列，求实数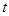
的值；
（2）设各项均不为0的数列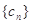
中，所有满足
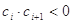的整数
的个数称为这个数列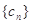的“积异号数”，令
（
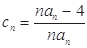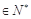），在（1）的条件下，求数列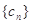的“积异号数”
相关试题
，
交椭圆C于A、B两点，求线段AB的长．
中，角A、B、C所对边分别是a、b、c，
，求
．（本小题满分12分）
设有两个命题p：关于x的不等式
（a > 0，且a ≠ 1）的解集是{ x | 
x < 0 }；
q：函数
的定义域为R．如果
为真命题，
为假命题，
求实数a的取值范围．
，
的定义域；
．
的前
项和为
， 已知
，
．
，证明数列
是等比数列；
，求数列
的前n项和推荐套卷
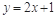数列的前n项和记为点在直线上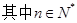，．（1）若数列是等比数列，求实数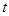的值；
（2）设各项均不为0的数列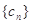中，所有满足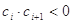的整数的个数称为这个数列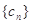的“积异号数”，令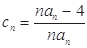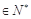（），在（1）的条件下，求数列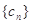的“积异号数”
（本小题满分12分）
设有两个命题p：关于x的不等式（a > 0，且a ≠ 1）的解集是{ x | x < 0 }；
q：函数的定义域为R．如果为真命题，为假命题，
求实数a的取值范围．
粤公网安备 44130202000953号