在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
相关知识点
推荐套卷
 中,∠
中,∠ 的平分线
的平分线 与△
与△ ,过
,过 ∥
∥ .
. 切线.
切线.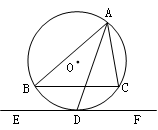
 、
、 、
、 、
、 ,其正面分别画有四个不同的几何图形(如图)小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.
,其正面分别画有四个不同的几何图形(如图)小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.
 、
、 、
、 ,其中
,其中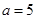 ,若关于
,若关于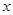 的方程
的方程 有两个相等的实数根,求△
有两个相等的实数根,求△ 的周长.
的周长.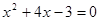 (用适当的方法);
(用适当的方法); (用配方法).
(用配方法). ,求代数式
,求代数式 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号