△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=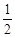 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
⑴ 求cosA的值.
⑵ 当以MN为直径的圆与△ABC一边相切时,求t的值.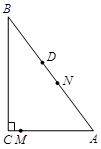
推荐套卷
△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD=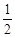 BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
⑴ 求cosA的值.
⑵ 当以MN为直径的圆与△ABC一边相切时,求t的值.