三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)。
17、(本小题满分10分)某校从参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40, 50),[50, 60),…,[90, 100] 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
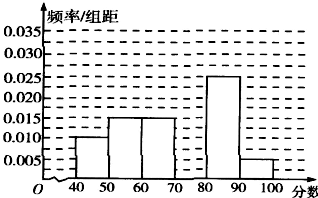
(I)求分数在 [70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ) 根据频率分布直方图估计这次高一年级期中考试的学生成绩的中位数(保留整数)。