为实施“农村留守儿童关爱计划”，某校结全校各班留守儿童的人数情况进行了统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅不完整的统计图：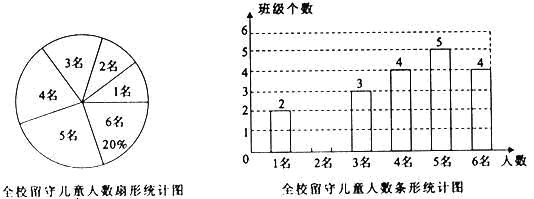
（1）求该校平均每班有多少名留守儿童？并将该条形统计图补充完整；
（2）某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率．
相关试题
识图理解：
请认真观察如图给出的未来一周某市的每天的最高气温和最低气温，直接回答后面提出的问题：
（1）这一周该市的最高气温和最低气温分别是多少?
（2）这一周中，星期几的温差最大?是多少?
人在运动时的心跳速率和人的年龄有关，如果用a表示一个人的年龄，
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数，那么有b=0．8（200-a），请问这个45岁的人某时心跳次数达到了122次，他有危险吗?为什么?
=-10,
=4,
=1的规律．求：
的值．
粤公网安备 44130202000953号