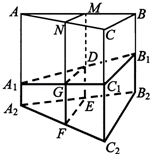
如图,某地质队自水平地面三处垂直向地下钻探,自点向下钻到处发现矿藏,再继续下钻到处后下面已无矿,从而得到在A处正下方的矿层厚度为.同样可得在处正下方的矿层厚度分别为,,且.过的中点且与直线平行的平面截多面体所得的截面为该多面体的一个中截面,其面积记为中.
(1)证明:中截面是梯形;
(2)在中,记边上的高为,面积为.在估测三角形区域内正下方的矿藏储量(即多面体的体积)时,可用近似公式估=中来估算.已知试判断估与的大小关系,并加以证明.
相关知识点
推荐套卷
 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
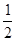 x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2,
x2-1的图像开口大小相同,开口方向也相同,y=f(x)的对称轴方程为x=1,图像过点(2, 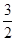 )点
)点 , x∈[3, 5]
, x∈[3, 5]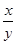 )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.
 ),f[f(-
),f[f(- )]值;
)]值; ,求x值;
,求x值; 粤公网安备 44130202000953号
粤公网安备 44130202000953号