给定椭圆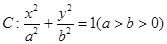
．称圆心在原点O，半径为
的圆是椭圆C的“准圆”．若椭圆C的一个焦点为
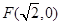，其短轴上的一个端点到F的距离为
．
(1)求椭圆C的方程和其“准圆”方程；
(2)点P是椭圆C的“准圆”上的一个动点，过动点P作直线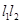
，使得
与椭圆C都只有一个交点，试判断是否垂直？并说明理由．
，
，
，求证：
。
、
、
两两异面，空间与
、
异面直线，
为空间任一点，过
与推荐套卷
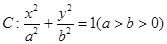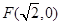给定椭圆．称圆心在原点O，半径为的圆是椭圆C的“准圆”．若椭圆C的一个焦点为，其短轴上的一个端点到F的距离为．
(1)求椭圆C的方程和其“准圆”方程；
(2)点P是椭圆C的“准圆”上的一个动点，过动点P作直线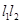，使得与椭圆C都只有一个交点，试判断是否垂直？并说明理由．
粤公网安备 44130202000953号