如图，已知菱形ABCD的边长为2，∠B=60°，点P、Q分别是边BC、CD上的动点（不与端点重合），且BP=CQ．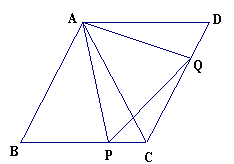
（1）图中除了△ABC与△ADC外，还有哪些三角形全等，请写出来；
（2）点P、Q在运动过程中，四边形APCQ的面积是否变化，如果变化，请说明理由；如果不变，请求出面积；
（3）当点P在什么位置时，△PCQ的面积最大，并请说明理由．
相关试题
；（2）
；（2）
.
，求a、m、n的值。
；
的图象上，点P（m，n）在
时，求P点的坐标；推荐套卷
如图，已知菱形ABCD的边长为2，∠B=60°，点P、Q分别是边BC、CD上的动点（不与端点重合），且BP=CQ．
（1）图中除了△ABC与△ADC外，还有哪些三角形全等，请写出来；
（2）点P、Q在运动过程中，四边形APCQ的面积是否变化，如果变化，请说明理由；如果不变，请求出面积；
（3）当点P在什么位置时，△PCQ的面积最大，并请说明理由．
粤公网安备 44130202000953号