已知椭圆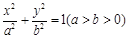 的离心率
的离心率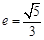 ,且直线
,且直线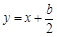 是抛物线
是抛物线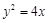 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P 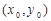 为椭圆上一点,直线
为椭圆上一点,直线 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线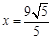 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
推荐套卷
已知椭圆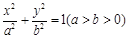 的离心率
的离心率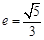 ,且直线
,且直线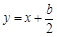 是抛物线
是抛物线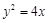 的一条切线.
的一条切线.
(1)求椭圆的方程;
(2)点P 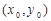 为椭圆上一点,直线
为椭圆上一点,直线 ,判断l与椭圆的位置关系并给出理由;
,判断l与椭圆的位置关系并给出理由;
(3)过椭圆上一点P作椭圆的切线交直线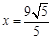 于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.
于点A,试判断线段AP为直径的圆是否恒过定点,若是,求出定点坐标;若不是,请说明理由.