已知直线 :
: 为参数), 曲线
为参数), 曲线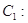
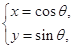 (
(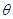 为参数).
为参数).
(1)设 与
与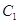 相交于
相交于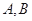 两点,求
两点,求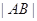 ;
;
(2)若把曲线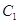 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的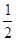 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的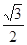 倍,得到曲线
倍,得到曲线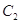 ,设点
,设点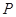 是曲线
是曲线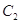 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
相关知识点
推荐套卷
已知直线 :
: 为参数), 曲线
为参数), 曲线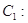
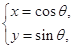 (
(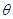 为参数).
为参数).
(1)设 与
与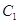 相交于
相交于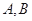 两点,求
两点,求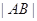 ;
;
(2)若把曲线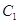 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的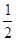 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的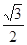 倍,得到曲线
倍,得到曲线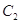 ,设点
,设点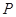 是曲线
是曲线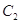 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.