某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次停止摸奖的概率；
（2）记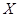
为1名顾客摸奖获得的奖金数额，求随机变量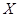的分布律和数学期望．
相关试题
－α）=－cosα；
，cos（α+β）=1，求证：cos（2α+β）=
．
，2kπ+π）（k∈Z），求角α的各三角函数值．推荐套卷
某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．
（1）求1名顾客摸球2次停止摸奖的概率；
（2）记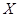为1名顾客摸奖获得的奖金数额，求随机变量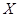的分布律和数学期望．
粤公网安备 44130202000953号