“初中生骑电动车上学”的现象越来越受到社会的关注，某校利用“五一”假期，随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法，统计整理制作了如下的统计图，请回答下列问题：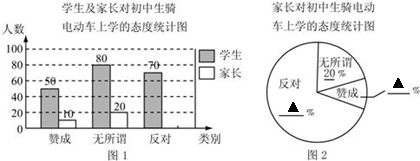
⑴这次共抽查了 个家长；
⑵请补全条形统计图和扇形统计图（友情提醒：条形图补画家长持“反对”态度的人数条，扇形图填上“反对”及“赞成”的百分数）；
⑶已知该校共有1200名学生，持“赞成”态度的学生估计约有 人．
相关试题
图为一位旅行者在早晨８时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象。根据图象回答问题：
在这个变化过程中，自变量是____，因变量是______。
９时，１０时３０分，１２时所走的路程分别是多少？
他休息了多长时间？
他从休息后直至到达目的地这段时间的平均速度是多少？
在下面的解题过程的横线上填空，并在括号内注明理由
如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.
解：∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
,求原长方形的宽。
、
和∠β（如图），利用直尺和圆规作ΔABC，使BC=
相关知识点
推荐套卷
粤公网安备 44130202000953号