如图所示,在平面直角坐标系中,抛物线 (
(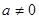 )经过
)经过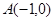 、
、 两点,抛物线与
两点,抛物线与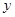 轴交点为
轴交点为 ,其顶点为
,其顶点为 ,连接
,连接 ,点
,点 是线段
是线段 上一个动点(不与
上一个动点(不与 、
、 重合),过点
重合),过点 作
作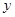 轴的垂线,垂足为
轴的垂线,垂足为 ,连接
,连接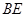 。
。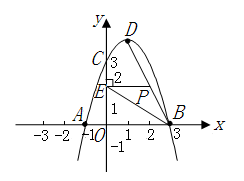
①求抛物线的解析式,并写出顶点 的坐标;
的坐标;
②如果 点的坐标为(
点的坐标为( ),
),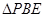 的面积为
的面积为 ,求
,求 与
与 的函数关系式,写出自变量
的函数关系式,写出自变量 的取值范围,并求出
的取值范围,并求出 的最大值;
的最大值;
③在②的条件上,当 取得最大值时,过点
取得最大值时,过点 作
作 的垂线,垂足为
的垂线,垂足为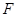 ,连接
,连接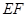 ,把
,把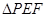 沿直线
沿直线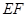 折叠,点
折叠,点 的对应点为
的对应点为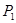 ,请直接写出
,请直接写出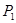 点坐标,并判断点
点坐标,并判断点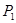 是否在该抛物线上;
是否在该抛物线上;
相关知识点
推荐套卷
 )
)


 ,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积.
,其余都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小颖从这3张背面朝上的卡片中任意摸出一张,然后计算小球和卡片上的两个数的积. 粤公网安备 44130202000953号
粤公网安备 44130202000953号