电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为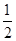 、
、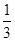 、
、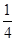 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.
(1)求该参加者有资格闯第三关的概率;
(2)求ξ的分布列和数学期望.
相关知识点
推荐套卷
电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为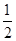 、
、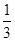 、
、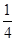 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.
(1)求该参加者有资格闯第三关的概率;
(2)求ξ的分布列和数学期望.