某选修课的考试按A级、B级依次进行,只有当A级成绩合格时,才可继续参加B级的考试.已知每级考试允许有一次补考机会,两个级别的成绩均合格方可获得该选修课的合格证书.现某人参加这个选修课的考试,他A级考试成绩合格的概率为 ,B级考试合格的概率为
,B级考试合格的概率为 .假设各级考试成绩合格与否均互不影响.
.假设各级考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得该选修课的合格证书的概率;
(2)在这个考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求
,求 的数学期望E
的数学期望E .
.
相关知识点
推荐套卷

 ,命题
,命题
 .若命题“
.若命题“ ”是真命题,求实数
”是真命题,求实数 的取值范围.
的取值范围. 的左、右顶点分别是
的左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 .若
.若 ,
, ,
, 成等比数列,求此椭圆的离心率.
成等比数列,求此椭圆的离心率.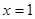 是函数
是函数 的一个极值点,其中
的一个极值点,其中 .
.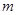 与
与 的关系式;
的关系式;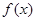 的单调区间;
的单调区间; 时,函数
时,函数 ,求
,求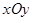 中,动点
中,动点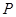 到两点
到两点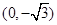 、
、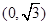 的距离之和等于4.设点
的距离之和等于4.设点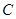 .
.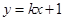 与
与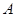 、
、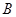 两点,若
两点,若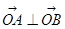 ,求
,求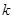 的值.
的值. -A BC中,AB
-A BC中,AB 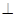 AC, AB=AC=2,
AC, AB=AC=2,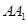 =4,点D是BC的中点.
=4,点D是BC的中点.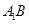 与
与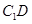 所成角的余弦值;
所成角的余弦值;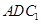 与
与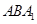 所成二面角的正弦值.
所成二面角的正弦值.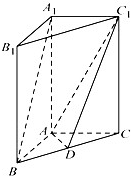
 粤公网安备 44130202000953号
粤公网安备 44130202000953号