一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出3次红球即停止．
(1)从袋中不放回地取球，求恰好取4次停止的概率P1；
(2)从袋中有放回地取球．
①求恰好取5次停止的概率P2；
②记5次之内(含5次)取到红球的个数为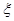
，求随机变量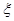的分布列及数学期望．
相关试题
表示两条直线,求m的值
过点(1,2)和第一,二,四象限,若
推荐套卷
一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出3次红球即停止．
(1)从袋中不放回地取球，求恰好取4次停止的概率P1；
(2)从袋中有放回地取球．
①求恰好取5次停止的概率P2；
②记5次之内(含5次)取到红球的个数为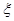，求随机变量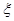的分布列及数学期望．
粤公网安备 44130202000953号