图是某市
月
日至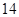
日的空气质量指数趋势图，空气质量指数（
）小于
表示空气质量优良，空气质量指数大于
表示空气重度污染，某人随机选择月日至月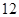
日中的某一天到达该市，并停留
天.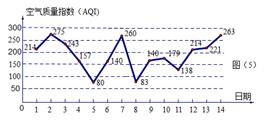
（1）求此人到达当日空气质量优良的概率；
（2）求此人停留期间至多有1天空气重度污染的概率.
}满足a
=1，
,求数列{a
}满足a
=1，a
a
+1（n≥2），求数列{a
前n项和
.
与
的关系；（2）求通项公式
中，
,
，求
。
，
，求
。推荐套卷
图是某市月日至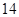日的空气质量指数趋势图，空气质量指数（）小于表示空气质量优良，空气质量指数大于表示空气重度污染，某人随机选择月日至月日中的某一天到达该市，并停留天.
（1）求此人到达当日空气质量优良的概率；
（2）求此人停留期间至多有1天空气重度污染的概率.
粤公网安备 44130202000953号