已知抛物线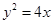 .
.
(1)若圆心在抛物线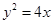 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线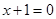 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线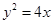 的焦点为
的焦点为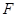 ,若过
,若过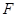 点的直线与抛物线相交于
点的直线与抛物线相交于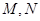 两点,若
两点,若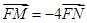 ,求直线
,求直线 的斜率;
的斜率;
(3)若过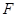 点且相互垂直的两条直线
点且相互垂直的两条直线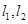 ,抛物线与
,抛物线与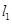 交于点
交于点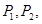 与
与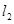 交于点
交于点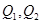 .
.
证明:无论如何取直线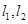 ,都有
,都有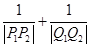 为一常数.
为一常数.
相关知识点
推荐套卷
已知抛物线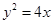 .
.
(1)若圆心在抛物线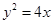 上的动圆,大小随位置而变化,但总是与直线
上的动圆,大小随位置而变化,但总是与直线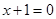 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;
(2)抛物线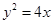 的焦点为
的焦点为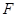 ,若过
,若过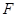 点的直线与抛物线相交于
点的直线与抛物线相交于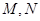 两点,若
两点,若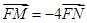 ,求直线
,求直线 的斜率;
的斜率;
(3)若过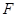 点且相互垂直的两条直线
点且相互垂直的两条直线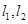 ,抛物线与
,抛物线与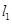 交于点
交于点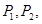 与
与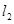 交于点
交于点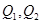 .
.
证明:无论如何取直线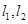 ,都有
,都有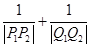 为一常数.
为一常数.